Koliko stupnjeva ima središnji kut pravilnog šesnaesterokuta?
Kojem pravilnom mnogokutu veličina središnjeg kuta iznosi 24° ?
Koliko stupnjeva ima središnji kut pravilnog petnaesterokuta?
Kojem pravilnom mnogokutu veličina središnjeg kuta iznosi 22° 30′ ?
Koliko stupnjeva ima svaki unutarnji kut pravilnog trideseterokuta?
Koliko stupnjeva ima svaki unutarnji kut pravilnog dvadeseterokuta?
Koliko stranica ima pravilni mnogokut kojemu je veličina unutarnjeg kuta 162° ?
Koliko stranica ima pravilni mnogokut kojemu je veličina unutarnjeg kuta 171° ?
Izračunaj veličinu vanjskog kuta pravilnog mnogokuta koji ima 24 vrha.
Izračunaj veličinu vanjskog kuta pravilnog mnogokuta koji ima 32 vrha.
Koliko ukupno dijagonala ima pravilni mnogokut kojemu je veličina vanjskog kuta 9° ?
Koliko ukupno dijagonala ima pravilni mnogokut kojemu je veličina vanjskog kuta 7° 30′ ?
Izračunaj veličinu unutarnjeg kuta pravilnog mnogokuta ako je veličina njegovog središnjeg kuta 7° 30′ .
Izračunaj veličinu unutarnjeg kuta pravilnog mnogokuta ako je veličina njegovog središnjeg kuta 12° .
Kojemu je pravilnom mnogokutu veličina središnjeg kuta osam puta manja od veličine unutarnjeg kuta?
Kojemu je pravilnom mnogokutu veličina središnjeg kuta pet puta manja od veličine unutarnjeg kuta?
Koliko stupnjeva imaju kutovi uz osnovicu karakterističnog trokuta pravilnog deseterokuta?
Izračunaj veličine kutova karakterističnog trokuta pravilnog deveterokuta.
Koliko stupnjeva imaju kutovi uz osnovicu karakterističnog trokuta pravilnog osmerokuta?
Izračunaj veličine kutova karakterističnog trokuta pravilnog peterokuta.
Kutovi uz osnovicu karakterističnog trokuta pravilnog mnogokuta imaju veličinu 80°. Koliko se dijagonala može nacrtati iz jednog njegovog vrha? Opseg i površina mnogokuta
Kutovi uz osnovicu karakterističnog trokuta pravilnog mnogokuta imaju veličinu 72°. Koliko se dijagonala može nacrtati iz jednog njegovog vrha? Opseg i površina mnogokuta
Pravilan mnogokut je svaki konveksni mnogokut kojemu su sve stranice jednake duljine i svi kutovi jednake veličine.
Veličina unutarnjeg kuta pravilnog mnogokuta:
Veličina unutarnjeg kuta pravilnog mnogokuta koji ima n vrhova iznosi $$ \frac{(n-2) \cdot 180^{o}}{n} $$ :
$$ \beta _{n}$$ = $$ \frac{(n-2) \cdot 180^{o}}{n} $$ .
Veličina vanjskog kuta pravilnog mnogokuta:
Veličina vanjskog kuta pravilnog mnogokuta koji ima n vrhova iznosi $$ \frac{360^{o}}{n} $$ :
$$ \beta _{n}^{'}_{}^{}$$= $$ \frac{360^{o}}{n} $$
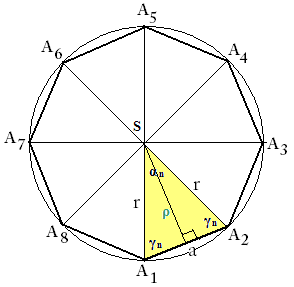
Karakteristični trokut pravilnog mnogokuta:
Karakteristični trokut pravilnog mnogokuta je trokut kojemu je jedan vrh središte pravilnog mnogokuta, a ostala dva vrha su bilo koja dva susjedna vrha tog mnogokuta.
Karakteristični trokut pravilnog mnogokuta je jednakokračni trokut kojemu je osnovica stranica tog mnogokuta, a kraci su dva polumjera njegove opisane kružnice.
Kutovi uz osnovicu karakterističnog trokuta dva su puta manji od unutarnjeg kuta tog mnogokuta:
$$ \gamma _{n}$$ = $$ \frac{1}{2} \cdot \beta _{n}$$ , $$ \gamma _{n}$$ = $$ \frac{(n-2) \cdot 90^{o}}{n} $$
Središnji kut pravilnog mnogokuta je kut kojemu je vrh središte tog mnogokuta, a kraci su mu dva polumjera mnogokutu opisane kružnice. Veličina središnjeg kuta pravilnog mnogokuta koji ima n vrhova iznosi $$ \frac{360^{o}}{n} $$:
$$ \alpha _{n}$$ = $$ \frac{360^{o}}{n} $$
Krak karakterističnog trokuta pravilnog mnogokuta polumjer je mnogokutu opisane kružnice, a visina karakterističnog trokuta polumjer je njegove upisane kružnice: