Primjer 1.: Nacrtan je pravokutnik ABCD. Točke K, L, M i N polovišta su njegovih stranica. Pomoću svih označenih točaka odredi sve vektore:
Zadatak 1.: Nacrtan je paralelogram ABCD. Točke E, F, G i H polovišta su njegovih stranica. Pomoću svih označenih točaka odredi sve vektore:
Primjer 2.: Nacrtan je romb ABCD. Točke E, F, G i H su polovišta njegovih stranica. Pomoću svih imenovanih točaka odredi sve vektore:
Zadatak 2.: Nacrtan je kvadrat ABCD. Točke K, L, M i N su polovišta njegovih stranica. Pomoću svih imenovanih točaka odredi sve vektore:
Primjer 3.: Zadan je vektor $$\vec {a}$$ i točka C. Nacrtaj vektor $$\vec {CD}$$ tako da bude jednak vektoru $$\vec {a}$$.
Zadatak 3.: Zadan je vektor $$\vec {c}$$ i točka C. Nacrtaj vektor $$\vec {AB}$$ tako da bude jednak vektoru $$\vec {c}$$.
Primjer 4.: Zadan je vektor $$\vec {b}$$ i točka E. Nacrtaj vektor $$\vec {EF}$$ tako da bude suprotan vektoru $$\vec {b}$$.
Zadatak 4.: Zadan je vektor $$\vec {d}$$ i točka C. Nacrtaj vektor $$\vec {CD}$$ tako da bude suprotan vektoru $$\vec {d}$$.
Primjer 5.: Nacrtanom kvadratu ABCD duljina stranice iznosi 3 cm. Sjecište dijagonala je točka S. Odredi duljine vektora:
Zadatak 5.: Nacrtanom pravokutniku ABCD duljine stranica iznose 4 cm i 2.5 cm.Sjecište dijagonala je točka S. Odredi duljine vektora:
Primjer 6.: Zadani su vektori $$\vec{a}$$ i $$\vec{b}$$. Nacrtaj vektor $$\vec{c}$$=$$\vec{a}$$+$$\vec{b}$$.
Zadatak 6.: Zadani su vektori $$\vec{e}$$ i $$\vec{f}$$. Nacrtaj vektor $$\vec{g}$$=$$\vec{e}$$+$$\vec{f}$$.
Primjer 7.: Zadani su vektori $$\vec{x}$$ i $$\vec{y}$$. Nacrtaj vektor $$\vec{w}$$=$$\vec{x}$$+$$\vec{y}$$.
Zadatak 7.: Zadani su vektori $$\vec{a}$$ i $$\vec{b}$$. Nacrtaj vektor $$\vec{c}$$=$$\vec{a}$$+$$\vec{b}$$.
Primjer 8.: Zadani su vektori $$\vec{m}$$ i $$\vec{n}$$. Nacrtaj vektor $$\vec{v}$$=$$\vec{m}$$+$$\vec{n}$$.
Zadatak 8.: Zadani su vektori $$\vec{g}$$ i $$\vec{h}$$. Nacrtaj vektor $$\vec{i}$$=$$\vec{g}$$+$$\vec{h}$$.
Primjer 9.: Nacrtan je paralelogram ABCD. Točka S je sjecište dijagonala $$\overline{AC}$$ i $$\overline{BD}$$. Promatrajući sliku, odredi:
Zadatak 9.: Nacrtan je pravokutnik ABCD. Točka S je sjecište dijagonala $$\overline{AC}$$ i $$\overline{BD}$$. Promatrajući sliku, odredi:
Primjer 10.: Zadani su vektori $$\vec{e}$$ i $$\vec{f}$$. Nacrtaj vektor $$\vec{g}$$=$$\vec{e}$$-$$\vec{f}$$.
Zadatak 10.: Zadani su vektori $$\vec{x}$$ i $$\vec{y}$$. Nacrtaj vektor $$\vec{w}$$=$$\vec{x}$$-$$\vec{y}$$.
Primjer 11.: Zadani su vektori $$\vec{k}$$ i $$\vec{l}$$. Nacrtaj vektor $$\vec{t}$$=$$\vec{k}$$-$$\vec{l}$$.
Zadatak 11.: Zadani su vektori $$\vec{m}$$ i $$\vec{n}$$. Nacrtaj vektor $$\vec{s}$$=$$\vec{m}$$-$$\vec{n}$$.
Primjer 12.: Zadani su vektori $$\vec{u}$$ i $$\vec{v}$$. Nacrtaj vektor $$\vec{s}$$=$$\vec{v}$$-$$\vec{u}$$.
Zadatak 12.: Zadani su vektori $$\vec{g}$$ i $$\vec{h}$$. Nacrtaj vektor $$\vec{j}$$=$$\vec{h}$$-$$\vec{g}$$.
Primjer 13.: Nacrtan je pravokutnik ABCD. Točka S je sjecište njegovih dijagonala. Pomoću imenovanih točaka odredi:
Zadatak 13.: Nacrtan je paralelogram ABCD. Točka S je sjecište njegovih dijagonala. Pomoću imenovanih točaka odredi:
Primjer 14.: Nacrtanom rombu ABCD točka S je sjecište dijagonala. Promatrajući sliku odredi vektore:
Zadatak 14.: Nacrtanom kvadratu ABCD točka S je sjecište dijagonala. Promatrajući sliku odredi vektore:
Primjer 15.: Zadani su vektori $$\vec{a}$$ i $$\vec{b}$$. Nacrtaj vektor $$\vec{a}$$+$$\vec{b}$$.
Primjer 16.: Zadani su vektori $$\vec{a}$$ i $$\vec{b}$$. Nacrtaj vektor $$\vec{a}$$-$$\vec{b}$$.
Primjer 17.: Zadani su vektori $$\vec{a}$$ i $$\vec{b}$$. Nacrtaj vektor $$\vec{b}$$-$$\vec{a}$$.
Usmjerena dužina ili vektor je dužina za koju je istaknuto koja je od njezinih krajnjih točaka početna, a koja završna.
Početna točka je hvatište vektora.
Pri crtanju vektora strelica se stavlja kod završne točke.
Orijentaciju vektora pokazuje njegova strelica.



O istoj ili suprotnoj orijentaciji vektora ima smisla govoriti samo ako vektori pripadaju istom ili usporednim pravcima, tj. ako su istog smjera (kolinearni).
Jednakost vektora:
Vektori su jednaki ako imaju jednake duljine, isti smjer i istu orijentaciju.
Suprotni vektori :
Vektori su suprotni ako imaju jednake duljine, isti smjer i suprotne orijentacije.

Nul – vektor :
Vektor koji počinje i završava u istoj točki naziva se nul – vektor.
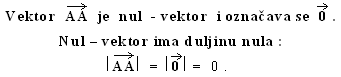
Zbrajanje vektora :

Oduzimanje vektora :






